Union Find один з базових алгоритмів і він демонструє як простий алгоритм може бути використаний для досить таки серйозних задач. Отож для початку я покажу малюнок для того щоб заманити вас почитати а далі перейду до пояснень.

https://www.facebook.com/note.php?note_id=469716398919
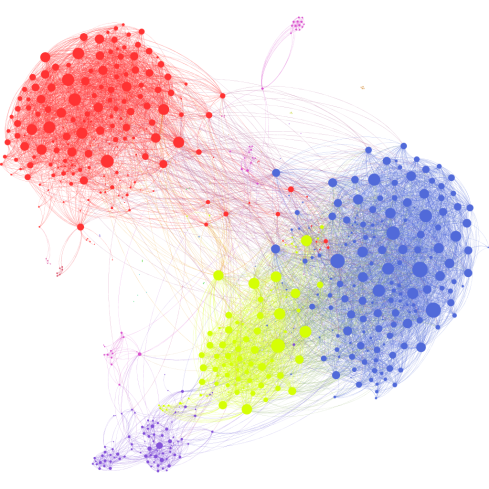
http://griffsgraphs.com/2012/07/02/a-facebook-network/
Ці малюнки фактично відображають звязки між користувачами в соціальних мережах, і працювати з ними досить таки важко, адже наприклад фейсбук має більше як пів мільярда активних користувачів. Павутина яку вони створюють дуже обємна її не те що важко описати її ще й потрібно обробляти, а обробка відбувається постійно. Часто в соц мережах ми можемо побачити повідомлення про те, що якась особа має з вами стільки то спільних друзів і можливо ви її знаєте. Отож побудований певний алогритм, який дає можливість просто визначити звязаних між собою людей навіть через декілька проміжних ланок.
Union Find дає змогу на основі звязків між елементами легко визначити чи будь який з величезного набору елементів звязаний з іншим елементом цього набору без використання купи циклів та інших “важких” операції.
Давайте розглянемо такий приклад:
Маємо вхідні дані:
Розмір масиву – 10
Звязки між елементами
1:2 2:3 3:4 8:2 5:7
Необхідно визначити чи елементи 1 та 8 зєднані та чи 0 і 5 зєднані.
Перш за все створимо масив:
індекси масиву: 0 1 2 3 4 5 6 7 8 9
дані в масиві : 0 1 2 3 4 5 6 7 8 9
Тут необхідне невеличке пояснення, перш за все індекси масиву це фактично положення елементів в масиві. Так як в сішарппі нумерація починається з 0 ми маємо відповідні індекси. Це незмінні дані які просто вказують на комірку масиву, відповідно якщо мені треба пятий елемент масиву я вказую індекс [5] тобто вказую індекс елементу який нам треба витягнути.
Дані в масиві я записав відповідно до їх положення в масиві, тобто в даному прикладі елемент за індексом [4] = 4.
В коді це виглядає досить просто:
1: class QuickFindUF
2: {3: int[] id = new int[10];
4: 5: public QuickFindUF()
6: {7: for (int i = 0; i < id.Length; i++)
8: { 9: id[i] = i; 10: } 11: } 12: .................................Ми просто в конструкторі заповнюємо масив необхідними даними.
Обєднання
Операція обєднування буде робити досить просту річ вона буде змінювати дані в масиві таким чином що значення записане за індексом буде вказувати на елемент з яким ця комірка звязана.
Виконаємо команду обєднування 1:2 в результаті обєднання ми отримаємо
індекси масиву: 0 1 2 3 4 5 6 7 8 9
дані в масиві : 0 2 2 3 4 5 6 7 8 9
Тобто елемент за індекосом [1] звязаний з елементом на який вказує його значення тобто з елементом за індексом [2]
якщо зараз ми виконаємо ще декілька обєдань то по черзі отримаємо
2:3
індекси масиву: 0 1 2 3 4 5 6 7 8 9
дані в масиві : 0 3 3 3 4 5 6 7 8 9
3:4
індекси масиву: 0 1 2 3 4 5 6 7 8 9
дані в масиві : 0 4 4 4 4 5 6 7 8 9
8:2
індекси масиву: 0 1 2 3 4 5 6 7 8 9
дані в масиві : 0 4 4 4 4 5 6 7 4 9
5:7
індекси масиву: 0 1 2 3 4 5 6 7 8 9
дані в масиві : 0 4 4 4 4 7 6 7 4 9
Отож після кроку 2:3 ми змінили всі числа 2 на 3, відповідно, якщо ми хочемо взнати чи 2 та 3 обєднані ми просто порівнюємо їхні значення в даному випадку значення за індексом [2] та значення за індексом [3] однакові що означає що вони звязані.
Наступний крок обєднав значення з індексами 3:4 ми пройшлись по масиву з змінили всі 3 на 4 відповідно тепер значення за індексами [1][2][3][4] містять однакові значення що означає що вони обєднані.
Крок 8:2 змінив значення в елементі за індексом [8] на 4 тобто ди до списку обєднаних елементів додали ще одни елемент. Тепер якщо взяти значення за індексами доприкладу [2] та [8] ми можемо їх досить леко порівняти і зробити висновок що це два елементи обєднані бо мають однакове значення.
Останнє обєднання 5:7 створило ще одну множину елементів візповідно змінивши значення за індексом [5] на 7.
Давайте опишемо код який робить це обєднання:
1: public void Union(int p, int q)
2: {3: int pid = id[p];
4: int qid = id[q];
5: 6: for (int i = 0; i < id.Length; i++)
7: {8: if (id[i] == pid)
9: { 10: id[i] = qid; 11: } 12: } 13: }Як бачимо ми просто приймаємо індекси елементів які необхідно обєднати беремо їхні дані, і проходячись по масиву замінюємо всі значення значення pid на значення qid. Це водночас найбільший недолік цієї реалізації, нам постійно необхідно проходитись по всьому масиву а це досить затратна операція.
Оптимальнішим варіантом виконання цього алгоритму буде не заміна всіх елементів в масиві на те з чим ми обєднуємо, а побудова дерева.
Я просто викладу варіант цього алгоритму і варіант Quick Union пропоную вам далі зрозібратись як вони працють.
Union Find
1: using System;
2: 3: namespace Quick_FindUF_2_2
4: {5: class Program
6: {7: static void Main(string[] args)
8: {9: QuickFindUF quickFind = new QuickFindUF();
10: 11: // Connecting
12: while (true)
13: {14: string leftItem = Console.ReadLine();
15: int p = int.Parse(leftItem);
16: 17: //ExitPoint
18: if (p == -1)
19: break;
20: 21: string rightItem = Console.ReadLine();
22: int q = int.Parse(rightItem);
23: 24: quickFind.Union(p, q); 25: 26: } 27: 28: // Check if points are connected.
29: string leftItem1 = Console.ReadLine();
30: int p1 = int.Parse(leftItem1);
31: 32: string rightItem1 = Console.ReadLine();
33: int q1 = int.Parse(rightItem1);
34: 35: if (quickFind.IsConnected(p1, q1))
36: {37: Console.WriteLine("Connected");
38: Console.ReadLine(); 39: } 40: } 41: } 42: 43: class QuickFindUF
44: {45: int[] id = new int[10];
46: 47: public QuickFindUF()
48: {49: for (int i = 0; i < id.Length; i++)
50: { 51: id[i] = i; 52: } 53: } 54: 55: public bool IsConnected(int p, int q)
56: {57: return id[p] == id[q];
58: } 59: 60: public void Union(int p, int q)
61: {62: int pid = id[p];
63: int qid = id[q];
64: for (int i = 0; i < id.Length; i++)
65: {66: if (id[i] == pid)
67: { 68: id[i] = qid; 69: }70: Console.Write("{0} ", id[i]);
71: } 72: Console.WriteLine(); 73: } 74: } 75: }Quick Union
1: using System;
2: 3: namespace Quick_Union_2_3
4: {5: class Program
6: {7: static void Main(string[] args)
8: {9: QuickUnion quickUnion = new QuickUnion();
10: 11: // Connecting
12: while (true)
13: {14: string readLine = Console.ReadLine();
15: int p = int.Parse(readLine);
16: int pRoot = quickUnion.FindRoot(p);
17: 18: string readLine1 = Console.ReadLine();
19: int q = int.Parse(readLine1);
20: int qRoot = quickUnion.FindRoot(q);
21: 22: //ExitPoint
23: if (p == -1)
24: break;
25: 26: quickUnion.Union(pRoot, qRoot); 27: 28: } 29: 30: // Check if points are connected.
31: string readLine2 = Console.ReadLine();
32: int p1 = int.Parse(readLine2);
33: 34: string readLine3 = Console.ReadLine();
35: int q1 = int.Parse(readLine3);
36: 37: if (quickUnion.IsConnected(p1, q1))
38: {39: Console.WriteLine("Connected");
40: Console.ReadLine(); 41: } 42: } 43: } 44: 45: internal class QuickUnion
46: {47: int[] id = new int[10];
48: 49: public QuickUnion()
50: {51: for (int i = 0; i < id.Length; i++)
52: { 53: id[i] = i; 54: } 55: } 56: 57: public void Union(int p, int q)
58: { 59: id[p] = id[q]; 60: 61: for (int i = 0; i < id.Length; i++)
62: {63: Console.Write("{0} ", id[i]);
64: } 65: Console.WriteLine(); 66: } 67: 68: public bool IsConnected(int p, int q)
69: {70: return id[p] == id[q];
71: } 72: 73: public int FindRoot(int item)
74: { 75: 76: while (item != id[item])
77: { 78: item = id[item]; 79: } 80: 81: Console.WriteLine("Root {0}", item);
82: return item;
83: } 84: } 85: }
Код на гітхабі: https://github.com/BatsIhor/Algorithms/
опис алгоритмів від Седжвіка рекомендую почитати : http://algs4.cs.princeton.edu/15uf/
Там можна знайти більше алгоритмів, я буду добавляти їх туди по мірі вивчення.
Будь які коментарі та зауваження вітаються )
No comments:
Post a Comment